ETC3250: Tutorial 2 Help Sheet

Exercises

Question 1

Part A to E

What is $X_{1}$ (variable 1)?
What is observation 3?
What is $n$ ?
What is $p$ ?
What is $X^{⊤}$ ?

Hint 1

Check week 1 lecture slides 19 to 25.

Hint 2

The notation section of the matricies wiki page might also help. The wiki page should also have a definition of the transpose.

Part F

Write a projection matrix which would generate a 2D projection where the first data projection has variables 1 and 4 combined equally, and the second data projection has one third of variable 2 and two thirds of 5.

Hint 1

Check week 1 lecture slides 26 to 31.

Hint 2

I would reccomend checking this page of the Cook and Laa textbook for the requirements of a projection matrix. Remember, matricies are just a simple way to describe a system of linear equations.

Hint 3

I would suggest writing the matrix that combines the variables correctly and then make sure it follows the gneeral requirements for a projection matrix. The projected data ( $Y$ ) should have dimension 1 equally variable 1 and variable 4, that is to say $Y_{1} = \frac{1}{2} X_{1} + \frac{1}{2} X_{4}$ and dimension 2 should be a third variable 2 and two thirds variable 5, that is $Y_{2} = \frac{1}{3} X_{2} + \frac{2}{3} X_{5}$ . Write these equations in matrix form to get a starting point for your answer.

Hint 4

The matrix equation that represents that linear system above is:

$\begin{array}{r} Y = XA = [\begin{array}{rrrrr} 2 & - 2 & - 8 & 6 & - 7 \\ 6 & 6 & - 4 & 9 & 6 \\ 5 & 4 & 3 & - 7 & 8 \\ 1 & - 7 & 6 & 7 & - 1 \end{array}] [\begin{array}{rr} 1 / 2 & 0 \\ 0 & 1 / 3 \\ 0 & 0 \\ 1 / 2 & 0 \\ 0 & 2 / 3 \end{array}] \end{array}$

This matrix has not been adjusted to fulfill the requirements of a projection matrix. If you are unsure how to convert this into a projection matrix, check the hints for Part G.

Part G

Why can’t the following matrix considered a projection matrix?

$\begin{array}{r} A = [\begin{array}{rr} - 1 / \sqrt{2} & 1 / \sqrt{3} \\ 0 & 0 \\ 1 / \sqrt{2} & 0 \\ 0 & \sqrt{2} / \sqrt{3} \end{array}] \end{array}$

Harriet’s Comment

The way this question is set up implies that we are asking why $A$ can’t be a projection matrix for $X$ , however that was not the intended question. Because of this implication, students often think the problem with this matrix is the dimensionality, (becuse the dimensions of $A$ and $X$ do not line up. This question is actually supposed to be asking about the validity of $A$ as a projection matrix in general, not specifically for $X$ .

Hint 1

(same as Hint 1 Part F) Check week 1 lecture slides 26 to 31.

Hint 2

(same as Hint 2 Part F) I would recommend checking this page of the Cook and Laa textbook for the requirements of a projection matrix. Remember, matricies are just a simple way to describe a system of linear equations.

Hint 3

The requirements for any projection matrix are:

The projected data should be a 2D matrix with n observations. Therefore the projection matrix has a specific dimensionality according to the rules of matrix multiplication which can be found on the wiki page.
The projection matrix should be orthonormal which means each column should be orthonomal with the other columns in the matrix. Remember, a vector cannot be orthogonal to itself.

Hint 4

The requirements for any projection matrix are (more specifically):

Since the data is $n \times p$ and the projected data needs to be needs to be $n \times p$ the projection matrix should have the dimension $p \times d$ . In this case, $d = 2$
Since $d = 2$ you only need to check each column is normalised (this will be two calculations) and the two columns are orthogonal to each other (this is just one calculation). A vector is normalised if it has a length of 1, i.e. $\sqrt{a_{11}^{2} + a_{12}^{2} + . . . + a_{1 n}^{2}} = 1$ . Two vectors are orthogonal to each other if their dot product is 0. That is, for columns i and j (where $i \neq j$ ) they need to satisfy: $a_{i} \cdot a_{j} = \sum_{k}^{n} (a_{i k} \times a_{j k}) = 0$ If you are unfamiliar with summation notation, this is just: $(a_{i 1} \times a_{j 1}) + (a_{i 2} \times a_{j 2}) + . . . + (a_{i n} \times a_{j n}) = 0$

Question 2

Which of these statements is the most accurate? And which is the most precise?

A. It is almost certain to rain in the next week.

B. It is 90% likely to get at least 10mm of rain tomorrow.

Hint 1

Check week 1 lecture slide 33 to see a diagram that depicts the difference between accuracy and precision

Hint 2

Accuracy tells you how likely a statement is to be true, and precision tells you how specific a statement is. For example, if I guess your weight to be somewhere between 0 and 1000kg, my statement is highly accurate (true with 100% certainty) but imprecise to the point of being meaningless. Typically a more accurate statement will be less precise, and a more precise statement will be less accurate.

Question 3

For the following data, make an appropriate training test split of 60:40. The response variable is cause. Demonstrate that you have made an appropriate split.

library(readr)
library(dplyr)
library(rsample)

bushfires <- read_csv("https://raw.githubusercontent.com/dicook/mulgar_book/pdf/data/bushfires_2019-2020.csv")
bushfires |> count(cause)

# A tibble: 4 × 2
  cause           n
  <chr>       <int>
1 accident      138
2 arson          37
3 burning_off     9
4 lightning     838

Harriet’s Comment

If you want to get the same results as the solution (that will eventually be posted) use set.seed(1156)

Hint 1

Check [week 1 lecture slides 34 to 36

Hint 2

Check the function initial_split with ?initial_split. Also look at the functions training and count to check your split and see how many are in each group.

Hint 3

Your function should use the options initial_split(data, prop=??, strata=??) to set an initial split. Then using testing(split) |> count(same variable you used for strata) to check the correct amount is in each group.

Question 4

In the lecture slides from week 1 on bias vs variance, these four images were shown.

(the images are in the tutorial, I’m not going to move them here)

Mark the images with the labels “true model”, “fitted model”, “bias”. Then explain in your own words why the different model shown in each has (potentially) large bias or small bias, and small variance or large variance.

Harriet’s Comment

The data in the images is testing data, so the model was not trained on it. Additionally, there is no error in the data generating process, that is to say, generated data is perfectly categorised according to the true model. Keep this in mind when considering the source of the error.

Chapter 2 of the ISLR textbook is of particular use for questions that require an understanding of the bias/variance trade off, such as this one.

Hint 1

Check week 1 lecture slides 44 to 54.

Hint 2

The black line is the true boundary (that generates the data), the colored dots show what the model has predicted. There is no noise so the wave function should perfectly categorise the observations.

Look for areas where there is error in the model (i.e. the coloured dots diverge from the from the true model) and try to work out what is causing them. Is the error bias, variance or irreducible? Try to explain if there is any common themes in the errors in the images.

Hint 3

The black Bias is caused by an inflexible model, variance is caused by a model that is too flexible. Error from bias will be predictable and consistent sources of error, error from variance will be inconsistent and hard to differentiate from irreduciable error. Error from bias is always visible in the images, error from variance only exists in repeated samples, however you should still mention it if you have used a highly flexible model.

Question 5

The following data contains true class and predictive probabilities for a model fit. Answer the questions below for this data.

#pred_data <- read_csv("https://raw.githubusercontent.com/numbats/iml/master/data/pred_data.csv") |>
#  mutate(true = factor(true))

Part A

How many classes?

Hint 1

Try using count() or table() or a similar function you are familiar with.

Part B

Compute the confusion table, using the maximum predictive probability to label the observation.

Hint 1

You have been given data that contains the true class, the probability an observation is class Adelie and the probability an observation is class Chinstrap. You need to make a new variable that represents the predicted class and add it to your data set. Then you need to use the predicted class and the true class to make a confusion matrix.

Hint 2

First use mutate() to add the predicted class to your data frame

The theory and code used to make a confusion matrix from a data set with the true and predicted values is shown on lecture 1 slides 37 to 39.

Part C

Compute the accuracy, and accuracy if all observations were classified as Adelie. Why is the accuracy almost as good when all observations are predicted to be the majority class?

Hint 1

Check lecture 1 slides 37 to 39. It shows you how to calculate accuracy by hand and with code.

Hint 2

To calculate the accuracy if if all observations were classified as Adelie, you can either use the formula on slide 30, or add a new variable where all the predictions are Adelie and calculate it with the code on slide 31.

Part D

Compute the balanced accuracy when all observations were classified as Adelie, by averaging the class errors. Why is it lower than the overall accuracy? Which is the better accuracy to use to reflect the ability to classify this data?

Hint 1

Again, check lecture 37 to 39. It shows you how to calculate the balaced accuracy by hand and with code.

Question 6

This question relates to feature engineering, creating better variables on which to build your model.

library(ggplot2)
library(ggbeeswarm)
spam <- read_csv("http://ggobi.org/book/data/spam.csv")
ggplot(spam, aes(x=spam, y=size.kb, colour=spam)) +
  geom_quasirandom() +
  scale_color_brewer("", palette = "Dark2") + 
  coord_flip() +
  theme(legend.position="none")

Part A

The following spam data has a heavily skewed distribution for the size of the email message. How would you transform this variable to better see differences between spam and ham emails?

Hint 1

Check lecture 1 slides 56. You can replace the skewed variable with its transformed version, however it is better practice to leave your data as is and only transform it in the model (or in this case, in the visualisation).

Hint 2

Try adding scale_y_log10() to the ggplot that generated the visual.

Part B

For the following data, how would you construct a new single variable which would capture the difference between the two classes using a linear model?

olive <- read_csv("http://ggobi.org/book/data/olive.csv") |>
  dplyr::filter(region != 1) |>
  dplyr::select(region, arachidic, linoleic) |>
  mutate(region = factor(region))
ggplot(olive, aes(x=linoleic, 
                  y=arachidic, 
                  colour=region)) +
  geom_point() +
  scale_color_brewer("", palette = "Dark2") + 
   theme(legend.position="none", 
        aspect.ratio=1)

Hint 1

To get an idea of what we are trying to do, look at the example in lecture 2 (not covered yet). Here is last years relevant slides, keel in mind they might be different to this year’s. Simply guessing and checking your results is a fair way to attempt this question. The remaining hints are going to explain how to find a solution without using guess and check.

You can also look at the theory section of this blog post, to get different visuals for what we are going to do. You do not need to understand LDA for this question (that will be covered in later weeks) so the body of the blog can be ignored, but the drawing of the two group projection and the animation following it might help you understand what we are doing here.

Hint 2

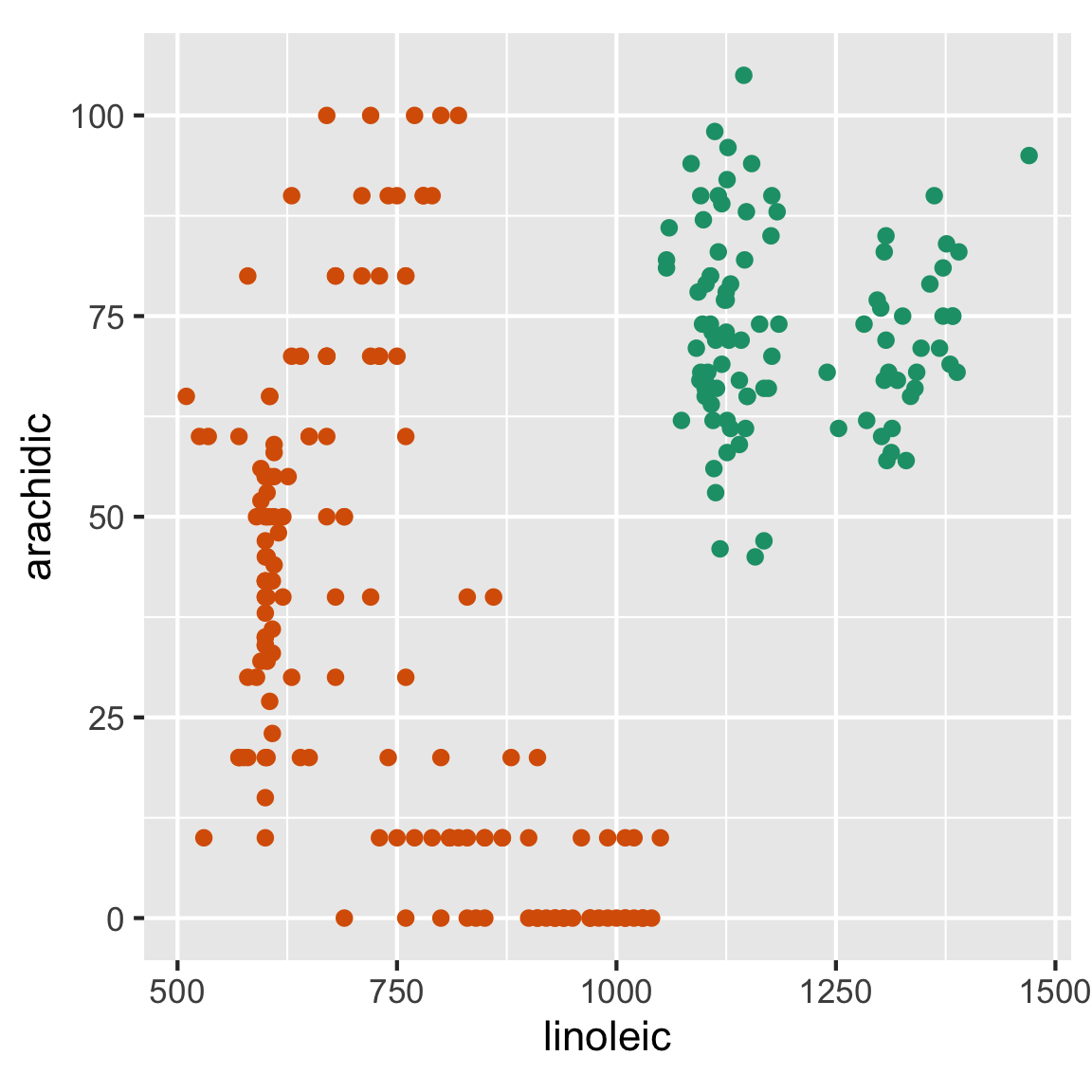
There are two ways to approach this problem. You can either find a line that separates the groups into two mounds (similar to what was done in lecture 2), or you can find a line that can be used as a decision boundary to separate the two groups (so each group is entirely contained on one side of the line). The line that is perpendicular to that decision boundary will be a good projection to separate the groups. The line that separates the two groups is what you want to project your data onto.

You can either manually calculate this line by looking at the plot and finding the slope with the visualisation. You may need to make a small change to the visualisation before hand to make this a tad easier.

When creating a new variable we only care about the proportions of the two variables, so the intercept of the line can be ignored. I would suggest using a plot that shows $y = a r a c h i d i c - 50$ and $x = l i n o l e i c - 1000$ so you don’t have to constantly be adjusting the intercept of your line when you want to change the slope.

Using the plot of your data, there are two methods that can be used to find the slope ( $m$ ) a line (this can be used reguardless of whether or not you are calculating the line that separates the two groups or the decision boundary). You can eyeball two points that should be on the line and use them to calculate $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ . Since the decision boundary and the separating projection are perpendicular, you can swap between the two slops using the relationship $m_{2} = \frac{- 1}{m_{1}}$ .

Alternatively you can use geom_abline() from ggplot2 to plot the line with a slope of $m$ and an intercept of $0$ (assuming you shifted your data). Note, geom_abline() should only be used to check the decision boundary. Since the axis in the plot are scaled 10x:1y, the angle is severely warped and a right angle on the plane will not be a right angle in the data visualisation. Thereofre, the correct separating line will look very wrong when you draw it on the plot. By this same token, if you plot the decision boundary its associated 1D projection, they will not appear perpendicular.

Hint 3

Once you have a nice separating line to project your data onto, you need to convert that to a projection vector. This is easy if you have your line in the form of $y = m x$ (still assuming $i n t e r c e p t = 0$ ). Projection vectors only require us to know the proportion of each variable we want in the projection. Our equation tells us the ratio $y : x$ is just $1 : m$ . If we normalise this to get a projection matrix, it will be $A = \frac{1}{1 + m} (1, m)$ . Then our new data can be expressed using the projection $Y = XA = (L i n o l e i c, A r a c h i d i c) \cdot (\frac{1}{1 + m}, \frac{m}{1 + m})$ .

You can add new variable in your data frame using the mutate function. To check if your projection is correct, you should plot it on a ggplot using geom_jitter() where x=new_variable and y=region. If you have a good projection, you should be able to mark draw a line on the x-axis that perfectly separates the data.

Question 7

Discuss with your neighbour, what you found the most difficult part of last week’s content. Find some material (from resources or googling) together that gives alternative explanations that make it clearer.